Going with the flow
In solving an age-old physics problem, a team led by Civil and Environmental Engineering’s Jerry Wang has helped enable a future permeated with nanoporous materials.
As anyone who has attempted to delve into the mysteries of the nanoscale world can attest, objects at the microscopic scale interact very differently than their larger counterparts. General principles taken for granted at the macroscale no longer apply when the distance between objects is not measured in meters, but in nanometers.
This phenomenon is becoming increasingly prevalent as more and more work is done in the field of nanoscale engineering. One example emerges from the no-slip boundary condition, used in fluid dynamics when modeling the flow of a fluid along a surface, such as water flowing through a pipe. Though this assumption has proven invaluable to scientists and engineers for over a century, more recent research has shown that this time-tested assumption can cause enormous errors when applied to fluid flows at the nanoscale. This poses a serious problem for researchers attempting to model nanofluidic flows through nano-porous desalination membranes, small-scale chemical analysis devices, or the intricate pore networks within rock and other structural materials.
A team of researchers led by Jerry Wang, assistant professor of civil and environmental engineering, has solved this physics quandary and removed a major obstacle to future modeling efforts for engineered nanostructures. In papers published by Physical Review Fluids in June and December of 2019, the team proposed and validated an equation that corrects the false assumptions made by the no-slip boundary condition.
As implied by its name, the no-slip boundary condition describes the tendency of fluids to move very little when in direct contact with a surface. Picture a straw: When liquid is drawn into the straw, the particles touching the inner sides remain in place, while those near the centerline are quickly drawn through. This “stickiness” at the boundary also explains why that last bit of toothpaste is so reluctant to leave the tube. As a result of this, scientists have long assumed in their calculations that the movement of fluid at this surface is effectively zero.
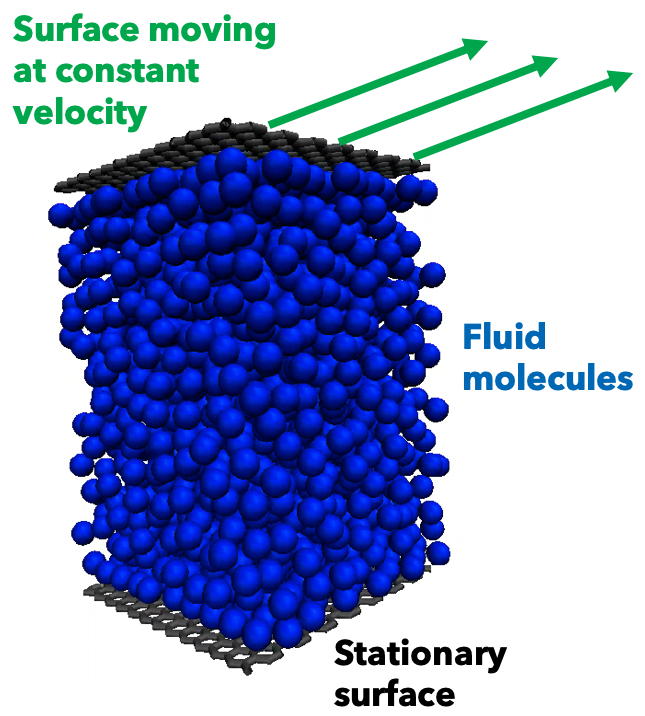
Source: College of Engineering
Fluid boundaries confined between two surfaces within a graphene nano-slit.
Nevertheless, there actually is a small degree of fluid movement, even at this seemingly stationary interface. This may be inconsequential when working in units of liters or gallons, but when measured in atoms, nanofluidic flow rates predicted assuming a no-slip boundary condition may be wildly off.
“The classical picture of a fluid says that there is essentially no flow at this boundary,” said Wang. “Here’s a loose analogy: If you have a narrow, three-lane highway, and the lane that merges into an exit ramp is slow-moving, you know that the overall flow of traffic is going to be pretty slow. But if the exit lane is moving faster, that bodes well for the overall traffic flow rate.”
Through molecular-dynamics simulations, Wang and his team discerned that the fluid and surface molecules interacted differently when compressed to nanoscale proportions. The degree of slip at the boundary depends on a host of factors, including the average fluid velocity, the extent to which the fluid likes to stick to the surface, and thermodynamic conditions like temperature and pressure. They found that slip can be accurately predicted using molecular-kinetic theory, producing a replacement for the no-slip boundary condition, thereby yielding a much more accurate prediction of the overall flow rate.
The ability of nanoporous materials to selectively admit molecules by size holds a potential breakthrough for chemical separations; these processes account for at least 10 percent of the world’s global energy consumption. Though we are only just beginning to recognize their full potential, this work will be a valuable tool for researchers modeling the next generation of nanofluidic technologies.
Wang’s research will continue exploring how more complex, non-homogenous fluids move at nanoscale proportions, and other factors that might affect fluid flow. With all the promise that nanofluidic technology holds, this small change in how we estimate fluid flow may well have big implications for the future.
